Les tables de multiplication

Il n’existe pas de techniques qui à elles seules, permettraient de mémoriser n’importe quoi, dans n’importe quelle condition. La mémoire, c’est l’aptitude à enregistrer des informations et la possibilité de les exprimer et de s’en servir pour se rappeler (mémoire orientée vers le passé) ou pour construire et faire des projets (mémoire orientée vers l’avenir). La mémoire, c’est une succession de 3 phases distinctes : l’entrée, le stockage et la sortie des informations.

Il existe quelques principes :

– Préciser très clairement aux élèves ce qui est à savoir, à retenir, à lire, à savoir-faire, … quand on leur donne une leçon à apprendre : projet d’apprendre. (Réseau d’images mentales)

– Mémoriser est plus facile si le contenu est intéressant et si on a compris (sens de l’apprentissage). Comprendre donc le sens de « multiplier » et de « fois ». Avoir une image mentale (quadrillage, rangées de…).

– Structurer les éléments, les organiser entre eux : proposer des activités de calcul variées et fréquentes qui stimulent l’intérêt des élèves et des situations de résolution fréquentes et progressives

– Accorder une place importante à la construction des automatismes.

– Répéter mécaniquement ne garantit pas la mémorisation.

Progression et stratégies d’apprentissage

table pythagore

On utilisera la commutativité : 2 fois 7, cela fait combien ? Et 7 fois 2 en même temps ; si je connais l’une, je connais l’autre.

Les tables de 2 (en rose) et de 5 (en bleu) sont les plus simples. La table de 2, ce sont les doubles, ils sont mémorisés avant même d’être traduits sous forme multiplicative. La table de 5 donne des nombres finissant par 0 (quand on multiplie par un nombre pair) ou par 5.

Les tables de 4 (en rouge) et 8 (en violet) sont ensuite bien placées, car on peut dire que la table de 4 est le double de la table de 2… On a ainsi un ordre: tables de 2, 4 et 8.

Ensuite, la mémorisation de la table de 9 (jaune clair) peut être facilitée par un certain nombre de remarques mnémotechniques du type : « Le chiffre des dizaines avance toujours de 1, alors que le chiffre des unités recule toujours de 1. Ex : 18, 27, 36… » Autre remarque : « Quand je dis 3 x 9 ? le résultat pour les dizaines c’est 3 moins 1, et pour les unités c’est le complément à 9. 27 deux sept. 6 x 9 : dizaine : 5, unité complément à 9, donc 54″.

Après, apprendre les tables de 3 et 6 qui forment un ensemble car 6 est le double de 3.

Et la table de 7 ? Et bien c’est fini, il n’y a plus rien à apprendre. Il ne reste plus que 7 x 7. C’est un carré qui est assez bien mémorisé.

Précisions didactiques

1 / Reconstruire les résultats

Pour mieux mémoriser, les élèves doivent savoir reconstruire les résultats. Comment reconstruire le résultat de 5 x 7 si je l’ai oublié ?

– soit en faisant référence au sens : en dessinant 5 paquets de 7 objets, en dessinant un rectangle de 5 sur 7 et en m’organisant pour compter les objets.

– soit en comptant 7 fois de 5 en 5, ou en comptant 5 fois de 7 en 7.

– soit je passe par 7 x 4 + 7.

Le lien entre additions répétées et multiplication est très important à installer, à maintenir chez les élèves.

=> Il faut reconstruire de manière calculatoire, en s’appuyant sur des résultats déjà connus. Cela doit être au cœur de l’apprentissage sur la multiplication.

2/ Les tables

Concernant la présentation des tables, il y a deux façons de procéder :

– soit on garde constant le multiplicateur :

Table de 4 : 4 × … donc : 4 × 1, 4 × 2, 4 × 3 , 4 × 4…

C’est celle qu’on trouve sur les « cahiers de brouillon » ou dans les outils commerciaux parascolaires. Ce sens s’appuie essentiellement sur la mémorisation.

– soit on garde constant le multiplicande :

Table de 4 : … × 4 donc : 1 × 4, 2 × 4, 3 × 4 , 4 × 4…

Ce sens s’appuie davantage sur le sens et permet de reconstruire les résultats. Si je connais 5 × 4 je pourrai trouver 6 × 4 car il « suffit » de rajouter 4 au résultat de 5 × 4.

La question de la formulation orale a aussi son importance. L’expression a × b peut se formuler de différentes façons :

– « a fois b » traduit une multiplication externe. « a » est le multiplicateur (nombre de fois) et « b » le multiplicande (nombre sur lequel on agit).

– « b fois a » traduit l’action de b sur le a : b est alors multiplicateur et a multiplicande.

– « a multiplié par b » traduit la multiplication interne. C’est une expression « neutre » qui n’induit aucun multiplicateur. L’élève doit alors faire la traduction la plus appropriée entre les deux précédentes selon son besoin.

Ainsi, par souci d’économie et de simplification, le choix est fait de traduire a × b par « a fois b » ou par « a multiplié par b ». La formulation « a fois b » peut toutefois être privilégiée car elle se rapproche davantage du sens et aide à la mémorisation. Ce choix n’a de sens qu’à une condition : présenter aux élèves ces différentes formulations et s’appuyer sur la commutativité de la multiplication.

C’est pourquoi dans MHM, les élèves travailleront sur différents outils : tables de multiplication, table de Pythagore, enveloppes cartons, etc.

3/ La table de Pythagore

On peut proposer une autre présentation de la table de Pythagore, qui rappelle le sens de la multiplication et permet d’illustrer la commutativité (en découpant les cases et en les superposant, par égalité de mesures) :

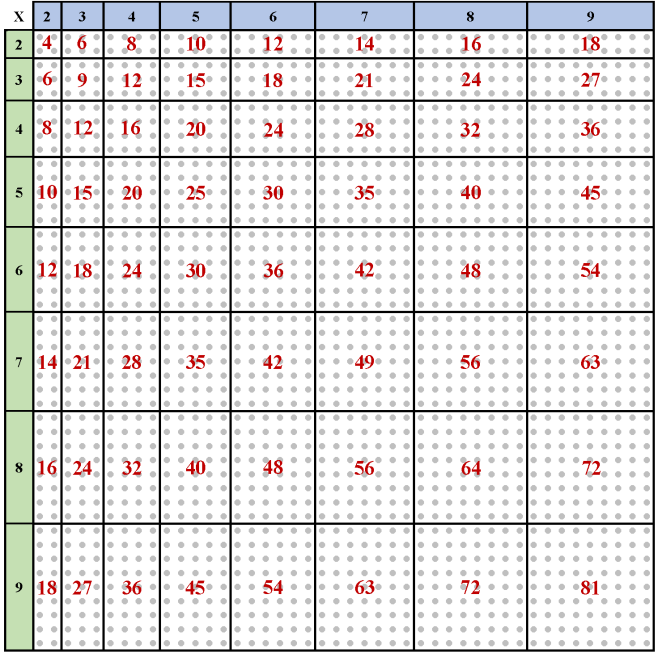
télécharger : TABLES IMAGEES 2
version sans les résultats: TABLES IMAGEES

Un autre élément qui semble important pour la mémorisation, c’est de donner à l’élève la conscience et la lisibilité de ce qu’il connaît par cœur et ce qu’il lui reste à mémoriser. Ce qu’on peut faire c’est par exemple de recommander à un élève de colorier dans sa table tout ce qu’il sait par cœur. Progressivement va s’imager pour l’élève ce qu’il sait et ce qu’il lui reste à apprendre. Cette lisibilité de ce que l’élève sait et de ce qu’il lui reste à apprendre peut être utile pour savoir sur quoi il doit travailler. C’est autre chose pour lui que d’apprendre la table de 2 alors qu’il la connaît aux trois quarts.

4 / L’entraînement et l’interrogation des résultats

La récitation des tables ne doit pas faire l’objet d’un travail trop systématique (nécessaire mais non suffisant) : cela favorise la mémorisation d’un bloc (il faudra alors réciter le tout pour retrouver un résultat). Les interrogations doivent être variées, diverses (formes) et fréquentes (quotidiennes – des temps courts).

Les modes d’interrogation doivent être multiples :

6 x 7 ?

? x 7 = 42 et ? x 6 = 42 et aussi ? x ? = 42

En 42 combien de fois 6 (de fois 7) ?

Questionnement du type QCM : 6×7 = ….13 ? ….42 ?…..67 ?

En CM, on ajoutera: 42 : 6 ? et 42 : 7 ?

La question de la formulation

C’est une question qui se pose régulièrement aux enseignants. 5 fois 6 est -il égal à 6+6+6+6+6 ou à 5+5+5+5+5+5 ? Est-ce la même chose que 5 multiplié par 6 ou que 6 multiplié par 5 ?

C’est plus complexe que cela en a l’air ! L’APMEP a réalisé un excellent article qui explicite cette question, alors bonne lecture : l’article.

Moyens mnémotechniques

Une petite vidéo qui explique comment retrouver toutes les tables de multiplication à partir de 5×6 sur nos deux mains !

Voir aussi: https://multimalin.com/

Apprendre les tables en vers:

En 1947, Jean Tardieu publie un recueil de poésies destiné aux enfants : « Il était une fois, deux fois, trois fois … ou La table de multiplication en vers » (Gallimard.

Gallimard l’a réédité sous le titre »Je m’amuse en rimant ».

Vidéo (Montessori):

Leçons pour apprendre les tables:

Le site « Tablettes et pirouettes » nous propose une présentation des tables intéressante pour l’entrainement individuel des élèves.

leçon-tables-480x640

Pour en savoir plus: http://www.tablettesetpirouettes.com/lecon-a-manipuler-sur-les-tables-de-multiplications/

Affichages et supports

Antonella Perucca, professeur (Department of Mathematics – University of Luxembourg) propose des affichages à imprimer (pour faire imprimer sur un mug, un poster…) :

http://www.antonellaperucca.net/easy-multiplication-tables.html

Apprendre avec des jeux / logiciels:

Jeu « multiplipotion » : voir ici

Et les jeux/applis numériques :voir ici

mais aussi l’appli « Défi tables » : lien