La soustraction posée ne doit pas être vue, comme les autres opérations, comme une technique à apprendre pour elle-même. La technique pour la technique, cela n’a aucun sens. C’est un outil pour résoudre des problèmes.
Concernant le sens:
Dans le « Ce qu’il faut savoir » du module 9, il est précisé:
Pour construire la soustraction, il faut travailler la mémorisation de résultats additifs, le travail des compléments, les dénombrements à rebours. La soustraction présente trois sens:
– le sens “enlever” : la soustraction correspond au calcul du reste d’une quantité d’objets. C’est le mieux compris et celui qu’on utilise pour introduire le signe. Cela peut se représenter en dessinant et barrant des représentations. Ce sens est adapté lorsqu’on enlève une petite quantité.
– le sens “pour aller à” : la soustraction correspond à calculer un complément. Cela correspond aux problèmes dans lesquels on cherche ce qu’on a ajouté ou une partie connaissant le tout et l’autre partie. Ce sens est adapté lorsqu’on enlève une quantité importante. Le recours à la bande numérique ou à la droite graduée est alors une méthodologie pertinente.
– le sens “écart” : la soustraction correspond à calculer un écart. Cela correspond aux problèmes de comparaison (combien de plus… ?).
Les trois sens seront travaillés progressivement sur l’ensemble du cycle 2.
Soyez rigoureux sur le vocabulaire et le langage mathématique : la « différence » c’est le résultat d’une soustraction, je peux retirer 8 à 4, ce n’est pas « impossible » mathématiquement…les mots « enlever/retirer/perdre » ne signifient pas forcément que le problème sera résolu par une soustraction (donc ne l’enseignez pas !).
Ne pas apprendre aux élèves qu’on calcule une soustraction en reculant systématiquement sur une file numérotée…La soustraction se calcule différemment selon les nombres: entre 103-8 et 103-96, on ne procède pas de la même façon ! Dans le premier cas, on fait des retraits successifs : 103 – 3 – 5. Dans le deuxième cas, on fait par complément : de 96 à 100 puis de 100 à 103. Il faudra aider les élèves à apprendre et utiliser ces deux stratégies dès le CP…
Concernant la technique:
Le premier point qu’il faudra enseigner tout au long de la scolarité des élèves est le fait qu’il ne faut pas toujours poser l’opération. Il est ridicule de poser 100 – 10 par exemple. Dans un certain nombre de cas, ce sera plus efficace par le calcul mental. Ce sera d’ailleurs comparé dans la méthode (module 21). Mais parfois, il faut poser ou c’est plus « facile » car en calcul mental, cela peut être cognitivement trop lourd pour certains élèves.
Il existe plusieurs techniques pour la soustraction posée lorsqu’il y a retenue. Avant d’aborder la technique, il faut être certain que les élèves savent écrire et poser proprement une opération. Pour les élèves en difficulté, il existe des outils -dys (cf article).
- La méthode française « traditionnelle », méthode « par compensation »:
L’idée est que la différence ne change pas si on ajoute simultanément un même nombre (en l’occurrence 10) aux deux termes d’une soustraction. Elle repose sur la propriété mathématiques: a–b = (a + c)–(b + c)
(ça peut s’illustrer par la droite graduée)
Elle est complexe à comprendre. Le « 10 » qu’on ajoute représente « 10 unités » en haut et « 1 dizaine » en bas. Ce double sens de la retenue est très peu compris par les élèves, y compris en CM. Ils sont incapables de l’expliquer généralement.

- La méthode anglo-saxonne « par emprunt » (« par cassage »):
Méthode par cassage : on casse une barre de dizaine, une plaque de centaine.
Méthode par emprunt: on s’appuie sur la règle d’échange 10 contre 1.

Je ne peux pas retirer 6 unités à 1 seule unité (à imager avec le matériel de numération). Donc je casse une des dizaines du nombre (ou j’échange). Je peux alors prendre 6 unités à 11. C’est une transformation de l’opération.
C’est une technique facile à comprendre car elle s’illustre très bien avec le matériel et qu’elle s’appuie sur les règles de numération.
Elle pose un problème d’écriture et de soin.
- La méthode par compléments (additions à trou):
Pour faire 61 – 17, je cherche :
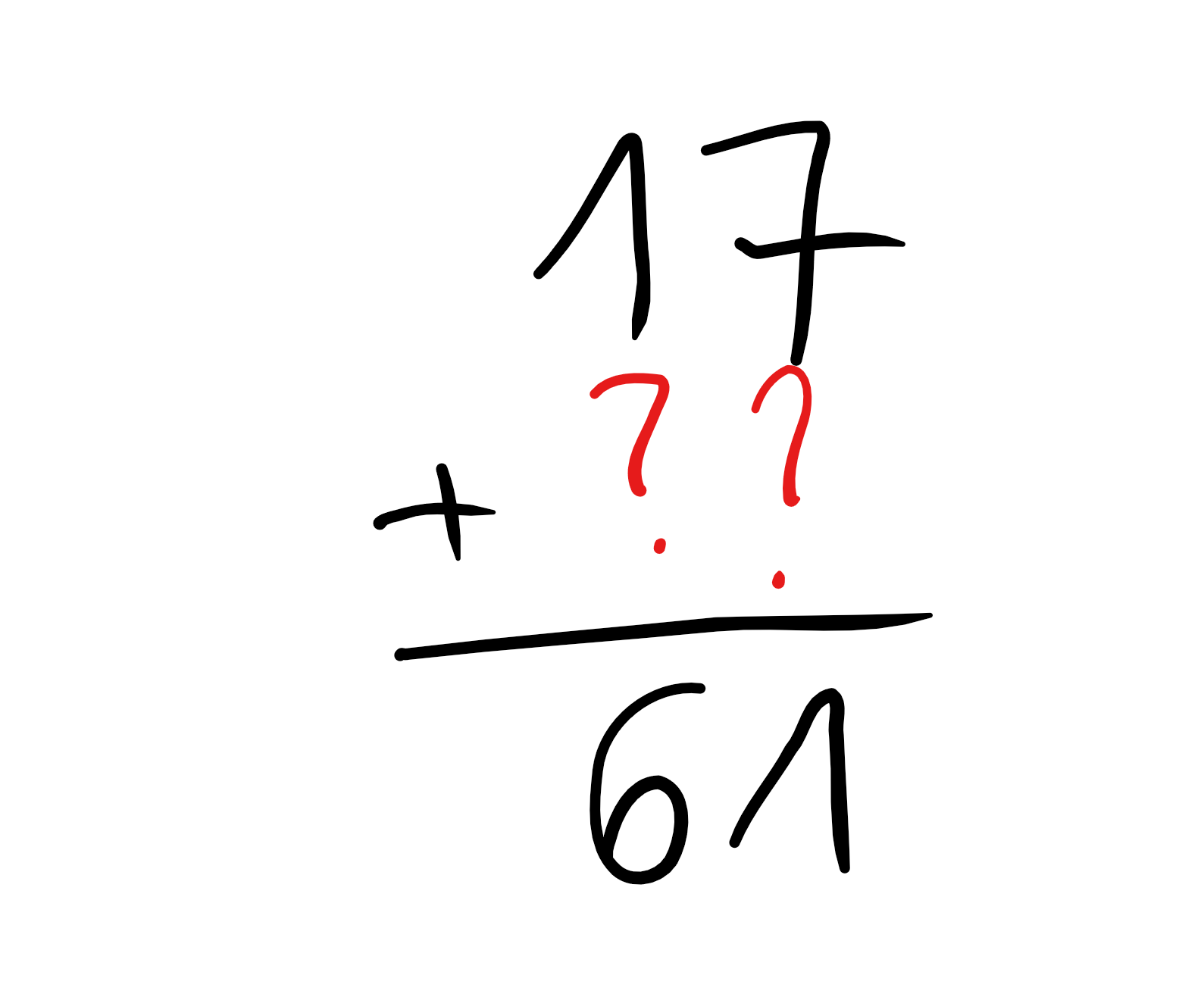
Sur le plan technique, c’est accessible car ce n’est qu’une adaptation d’une technique qu’ils connaissent déjà ! Mais la construction du sens est difficile et ils ont parfois du mal à faire du sens…
Comparaison des méthodes
| Technique traditionnelle | Technique par cassage | Technique par compléments | |
| Avantages | Efficace si beaucoup de retenues. | Facile à expliquer avec le matériel.Associée à un sens facile de la soustraction (retrait). Permet de faire le lien avec la numération. Image mentale plus aisée pour l’élève. | S’appuie sur une technique connue. |
| Inconvénients | Compréhension du fonctionnement difficile (place des retenues, double sens des retenues).Lien avec la numération peu explicite.Plus liée aux problèmes de comparaison. | Difficile à gérer dans certains cas avec plusieurs retenues.Problèmes d’écriture (aussi dans la division posée en CM) | La transposition de l’addition à trous en soustraction est difficile.Ce n’est qu’une étape intermédiaire. Il faut apprendre une technique posée… |
La question de la taille des opérations
Certains argumentent sur la nécessité de choisir la technique traditionnelle car avec les grands nombres cela fait trop de retenues avec la technique anglo-saxonne…Cela pose implicitement la question de la taille des opérations qu’on donne à faire aux élèves. Si on veut vérifier la technique et la capacité à mettre en œuvre l’algorithme, point besoin d’opérations « délirantes » (du type 103 214 – 57893) qui vont juste augmenter statistiquement le risque d’erreurs…et avec toute méthode et dont l’intérêt est …?
Je rappelle que dans les programmes de maths de Singapour on ne donne pas d’additions/soustractions avec des nombres de plus de 4 chiffres !
Le choix de la méthode heuristique est celui de la méthode anglo-saxonne, associée à une réflexion sur la nécessité ou non de poser l’opération. En effet, il faut apprendre à l’élève à réfléchir et analyser : ai-je besoin de poser l’opération pour faire 1000 – 134 ? Non ! Ce sera travaillé et encouragé dans la méthode…pour que la technique posée ne soit pas systématique mais à bon escient ! (Tout comme, on ne posera pas 1 034 656 – 798 099 …on prendra la calculatrice !)
Pour ceux qui oseraient …
Lors de l’expérimentation de MHM, il avait été réfléchi à des techniques alternatives : la multiplication indienne et une version « basique de la soustraction » illustrée ci-dessous:

Il suffit « juste » de soustraire : 1 unité – 7unités donne -6, soit un déficit de 6 (j’avais un cube, on m’en demande 7 donc j’en dois 6)…on travaille ensuite sur les dizaines : 9 dizaines auxquelles j’ôte une dizaine donne 8 dizaines… En le traduisant comme sur la photo ça redonne du sens aux élèves (9d-1d=90-10)
L’avantage de cette méthode est qu’on peut même commencer par les dizaines , puis faire les unités…Il n’y a plus de retenue…le restant de l’opération étant une soustraction « facile » car c’est un complément…
à mon sens, elle ne présente que des avantages mais deux gros inconvénients : la gestion des nombres « négatifs » (on peut y échapper en passant par la verbalisation) et surtout le rejet des adultes trop décontenancés par cette approche…Bref au final, elle fut abandonnée (comme la multiplication indienne) dans la version « finale » de MHM…
Représentation matérielle/ visuelle
Pour aider à la compréhension le matériel de numération sera précieux pour faire sens entre les actions sur les nombres et le sens.
Les vidéos de MHM
Sur la chaine youtube, vous trouverez deux vidéos sur la technique:
Vidéo sur le sens :
Vidéo sur la technique (sans retenue) :
Vidéo sur la technique (avec retenue):
Les vidéos des fondamentaux
Canopé propose 6 vidéos sur la soustraction pour le cycle 2:

Pour aller plus loin
– Article de l’APMEP : la soustraction à l’école élémentaire
– Extraits du guide du maitre de « J’apprends les maths avec Tchou » de R Brissiaud (voir à partir de la page 23 pour la soustraction)